Reductions

In computability theory and computational complexity theory, a reduction is an algorithm for transforming one problem into another problem. A sufficiently efficient reduction from one problem to another may be used to show that the second problem is at least as difficult as the first.

Intuitively, what does this mean?

Let’s say we have two problems $f$ and $g$. Let’s suppose that problem $g$ has a known solution. Then the following is a reduction from $f \to g$.

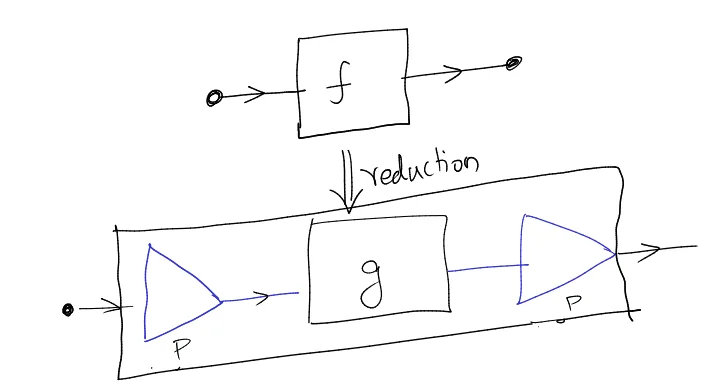
The “Reduction” is basically finding those two blue boxes, which convert the input and output from that of problem $f$ to equivalent input for problem $g$. Now we can simply compute the solution for problem $g$ and then use the reverse of our reduction algorithm to transform the output to that required by $f$.

If we can find two such blue triangles which can transform the input & output in such a way then we can effectively say that problem $f$ has been reduced to solving problem $g$. This is because solving $g$ implies being able to solve $f$.

What’s more interesting is if these blue triangles are polynomial-time algorithms. If we can find poly-time algorithms which can perform this transformation of the input and output, then we have an efficient reduction.

We have effectively managed to solve $f$ using the solution of $g$, along with some (hopefully efficient) pre and post-processing.

References

These notes are old and I did not rigorously horde references back then. If some part of this content is your’s or you know where it’s from then do reach out to me and I’ll update it.

1. A discussion with Anurudh Peduri on the Theory Group Discord.