This is one of the most famous unsolved questions in computer science. I mean, seriously, the clay math institute offers a reward of a million dollars to the first person that is able to solve this problem. https://www.claymath.org/millennium-problems/p-vs-np-problem

Why? What’s so special about this problem and what even is the problem?

Let’s begin by defining the problem. The problem asks, is $P = NP$? That is, is the set of all the problems in $NP$ the same as the set of all the problems in $P$? A more intuitive way to phrase this question would be asking, “Are all problems that can be verified in polynomial time, also be solved in polynomial time?”

But why is this one of the most famous unsolved problems in computer science? What are the implications of such a result? Why is this even a question, do we even have any reason to believe that $P$ might equal $NP$?

Here are a few, interesting answers to these questions.

1. If $P$ did equal $NP$, it would mean that simply being able to check if a solution is correct, would be no harder than solving the problem itself. Optimization problems like transport routing, production of goods, circuit design, etc. are all $NP$ problems. We would be able to get optimal answers to these solutions much faster than we are able to today. The economy could be made so much more efficient. Protein folding is an $NP$ problem. If we could make protein folding a problem in $P$ then we would be able to make huge breakthroughs in biology. We would be able to cure cancer! One of my favorite quotes describing the implications of $P=NP$ is from an MIT researcher,

   “If P=NP, then the world would be a profoundly different place than we usually assume it to be. There would be no special value in “creative leaps,” no fundamental gap between solving a problem and recognizing the solution once it’s found. Everyone who could appreciate a symphony would be Mozart; everyone who could follow a step-by-step argument would be Gauss; everyone who could recognize a good investment strategy would be Warren Buffet.” - Scott Aaronson

   One small downside is that RSA is also a $NP$ problem. If $P=NP$, all known security encryption measures would breakdown and none of our passwords would be safe :)

2. But the truth is, most computer science researchers do not believe that $P=NP$. Consider the first definition of $NP$ problems that we gave. We are essentially relying on non-determinism in our Turing machine. We are relying on the fact that the Turing machine is somehow able to “magically” or “luckily” always pick the right path of traversal. Luck or magic is not something we can model in a deterministic Turing machine. However, despite all this, no one has been able to prove $P \neq NP$.

3. Finally, problems in $NP$ have indeed been shown to be in $P$. Consider sorting an array by going through all its different permutations, such an algorithm would take $O(n!n)$ time. It is not in $P$. However, after we cleverly came up with a better algorithm such as bubble sort or merge sort, we managed to reduce this problem to be in $P$ by coming up with an $O(nlogn)$ algorithm for solving it. Similarly, problems we once thought to be in $NP$ have been shown to be in $P$ after someone managed to come up with a clever algorithm to solve the problem faster. But just because some problems we thought to be in $NP$ were later found to be in $P$ , does not mean that the two classes are equal. In fact, that the question $P=NP$ ? is really asking is if $P = NP-Complete$. Recall that $NP-Complete$ problems are the hardest problems in $NP$. Every single problem that belongs in $NP$, including the $NP-Complete$ problems are reducible to an $NP-Complete$ problem. This means that if we could somehow reduce even one problem belonging to the $NP-Complete$ class to $P$, we would be able to prove $P=NP$. So far, problems in $NP$ were found to be reducible to $P$, but never an $NP-Complete$ problem. As mentioned on the Clay institute website, “However, this apparent difficulty may only reflect the lack of ingenuity of your programmer.” Someday, someone just might be able to come up with a radical new algorithm to reduce one of the $NP-Complete$ problems to $P$. There is a possibility, even if highly unlikely.

This is a view of the complexity classes as we know it, depending on the result of the $P$ vs $NP$ problem.

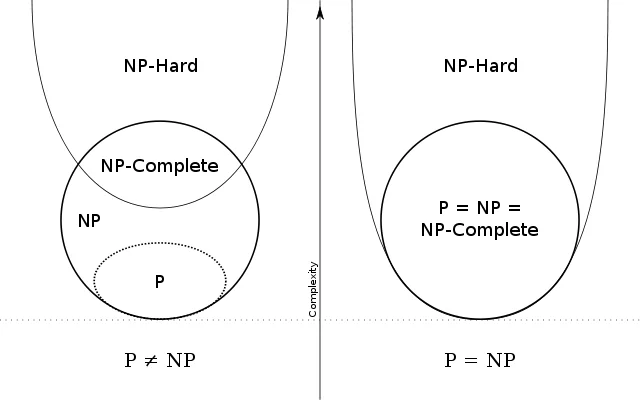
Courtesy: https://brilliant.org/wiki/complexity-classes/

References

These notes are old and I did not rigorously horde references back then. If some part of this content is your’s or you know where it’s from then do reach out to me and I’ll update it.

1. Professor Kannan Srinathan’s course on Algorithm Analysis & Design in IIIT-H
2. Why We Might Use Different Numbers in the Future - Up and Atom (Great Channel, recommend checking out)
3. Complexity Classes - Brilliant.org