Vectorization

The basic idea behind vectorization is just SIMD from Flynn’s Taxonomy. It allows us to perform the same instruction on multiple data element in parallel. This is achieved in hardware because of the existence of extended register files on the CPU. The CPU is modified to contain registers which can be anywhere from 128-512 bits or even larger (GPUs). These 512 bit registers can load 512 bits of data in one instruction and packed add $\frac{512}{32} = 16$ floating point additions in one instruction.

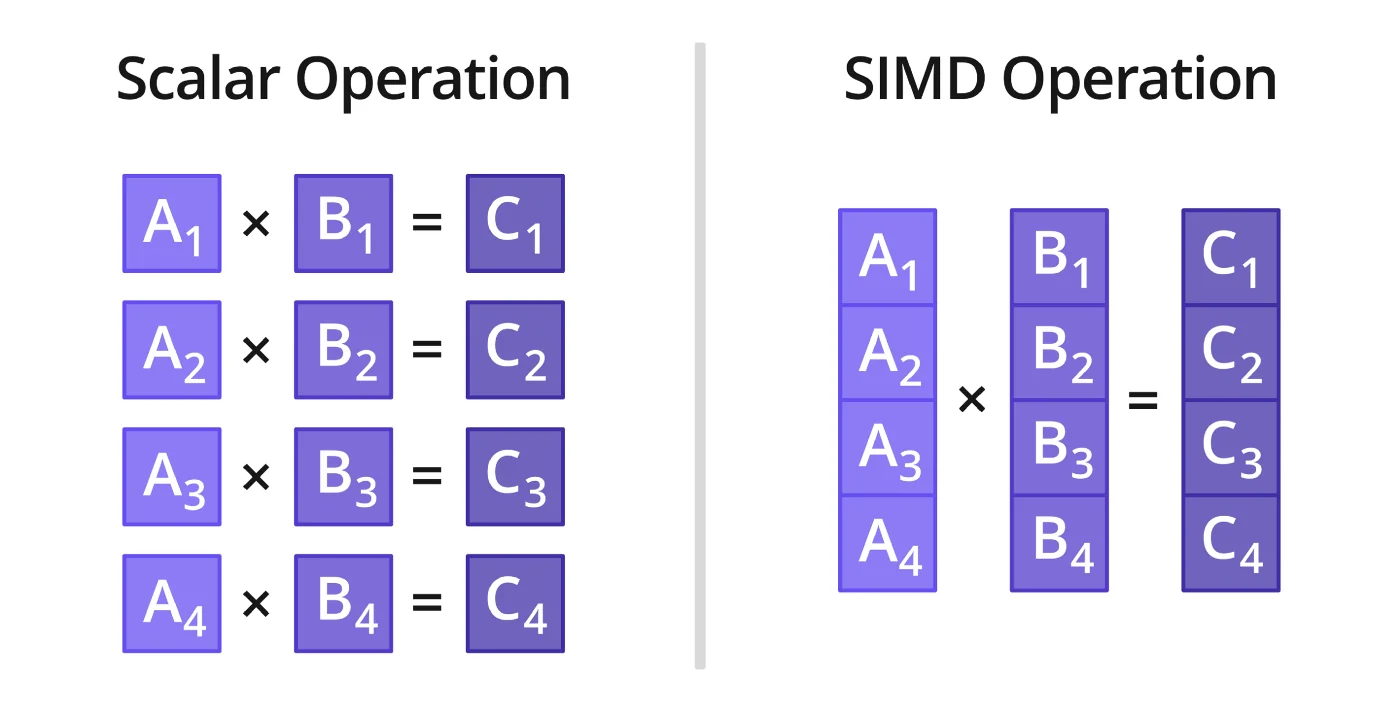
simd-1

A comprehensive list of all the SIMD instructions can be found here.

Memory alignment

When memory is aligned to 32/64 bit word boundaries than we can expect our effective memory bandwidth to be higher. When memory is fetched into the CPU cache line it is fetched in cache line sizes which are usually 64 bytes long. When data is not aligned to some nice power of 2, there will be multiple scenarios when our data element crosses a cache boundary and hence forces the compiler to make 2 fetches as the cache line does not contain the entire data element.

AVX loads expect 16/32 bit alignment of memory for the normal load / store instructions. You’d have to use special uload to load from unaligned memory. This might be slower.

Loop unrolling

Loop unrolling can be done automatically by the compiler and is also often used by programmers to speedup for loops. For example, consider the following code

for(int i=0; i<n; i++)
		c[i] = a[i] + b[i]

This code can be unrolled to

for(int i=0; i<n-4; i+=4){
		c[i] = a[i] + b[i];
		c[i+1] = a[i+1] + b[i+1];
		c[i+2] = a[i+2] + b[i+2];
		c[i+3] = a[i+3] + b[i+3];
}

Suddenly this code becomes vectorize-able. Loops can be unrolled by the compiler if it decides it is worth it.

Advantages

There are 2 main reasons to want to vectorize loops.

Lesser conditional statement execution. Notice that in the unrolled loop the conditional check i<n runs n times. Conditional statements are bad as they could introduce a potential branch in the code path. Usually branch predictors are good enough to cut back on major losses but it still helps to reduce the execution of the conditional check to $\frac{n}{4}$ times.
Facilitate register renaming. The compiler can use its full set of registers to perform load and store operations out of order to speedup execution of some of these instructions. For example, you can now perform multiple reads to different src registers and then perform writes during the store of other values. Compilers can recognize such opportunities and employ register renaming here. This would not be possible in unrolled loop code.

Disadvantages

The primary disadvantage is increase in code size. Increased code size could potentially increase the number of instructions the CPU has to load into it’s instruction cache and hence lead to some slowdown. Another obvious disadvantage is that the code looks terrible.

Pointer Aliasing

Sometimes, given code like this

void *element_sum(int *a, int *b, int N){
		for(int i=0; i<N; i++) a[i] = a[i] + b[i];
}

The compiler might not be able to parallelize it due to aliased pointers. Essentially, the compiler has no guarantee that pointers a and b point to two independent arrays. The vectorized code would give incorrect results if b pointed to some element of a itself. Hence it will not explicitly auto vectorize the code unless given some form of guarantee, usually via a restricted pointer or pragmas like pragma ivdep (for GCC).

Dependence Analysis

True (flow) dependence (RAW → Read after Write)
```
1: a = 1;
2: b = a;
```
Anti dependence (WAR → Write after Read)
```
1: b = a;
2: a = 2+b;
```
Output dependence (WAW → Write after Write)
```
1: a = 1;
2: a = 2+b;
```

If $S_j$ is dependent on $S_i$, we write $Si \ \delta \ S_j$. Sometimes we also indicate the type of dependence using superscript. $\delta^f, \ \delta^a, \ \delta^o$.

Loop carried dependence

for i = 1 to 3:
		x[i] = y[i] + 1
		x[i] = x[i] + x[i-1]

This update requires x[i] to know the value of x[i-1] beforehand. This is a loop carried dependence and cannot be parallelized easily.

Key points:

True (flow), anti, and output dependences are identified based on the order of read and write operations.
Loop-carried dependences arise when an iteration depends on the result of a previous iteration, hindering parallelization.
Dependence analysis is crucial for identifying parallelization opportunities and potential data hazards.

An Algorithm to Test for Dependence

Take the read set and write sets of 2 consecutive iterations and check for dependence. If there is an intersection between $R_{s1}$ and $W_{s2}$ or $W_{s1}$ and $R_{s2}$ then there is an dependence.

Example,

for(int i=16; i<n; i++)
		a[i] += a[i-16]

Take, $R_{s1} = \{ a[16], \ a[0]\}$, $W_{s1} = \{ a[16]\}$ and $R_{s16} = \{a[32], a[16]\}$, $W_{s16} = \{a[16]\}$. There is dependence.

For iterations $s1$ and $s16$:

$R_{s1} = {a[16], a[0]}$
$W_{s1} = {a[16]}$
$R_{s16} = {a[32], a[16]}$
$W_{s16} = {a[32]}$

Since $W_{s1}$ and $R_{s16}$ intersect at $a[16]$, there is a data dependence.

The key steps are:

Identify read and write sets for consecutive iterations.
Check for intersections between the read set of one iteration and the write set of the other iteration, or vice versa.
If an intersection exists, there is a data dependence.

Loop Un-Switching

for(int i=0; i<n; i++)
		for(int j=0; j<m; j++)
				if(x[i] > 0) // S++
				else // T++

Code like this can be converted to

for(int i=0; i<n; i++)
		if(x[i] > 0)
				for(int j=0; j<m; j++) // S++
		else
				for(int j=0; j<m; j++) // S++

The idea is that we eliminate repeated conditional branch checks from inside the for loop. The execution of the branch statement is reduced from $n \times m$ times to $n$ times, while the loop iterations is increased from $n \times m$ to $n \times 2 \times m$. But usually the internal loop can now employ vectorization thanks to the removal of the conditional statement to essentially reduce loop iterations to $\frac{n \times m \times 2}{vec \ len}$.

This gives the added speedup from vectorization + the speedup from lesser execution of conditional branch statements.

Index Set-Splitting

The concept of index set-splitting can be better illustrated with a practical example. Let’s consider a scenario where you have an array of integers, and you want to perform a specific operation on the even-indexed elements and a different operation on the odd-indexed elements. This situation often arises in image processing or signal processing algorithms. Suppose we have the following code:

int arr[] = {1, 2, 3, 4, 5, 6, 7, 8};
int n = sizeof(arr) / sizeof(int);

for (int i = 0; i < n; i++) {
    if (i % 2 == 0) arr[i] *= 2;
    else arr[i] /= 2;
}

This code flow includes conditionals within the loop iteration which makes it difficult to vectorize. But compilers can use index set-splitting here to split the loop into two separate loops, one for even-indexed elements and another for odd-indexed elements, as follows:

int arr[] = {1, 2, 3, 4, 5, 6, 7, 8};
int n = sizeof(arr) / sizeof(int);

for (int i = 0; i < n; i += 2) arr[i] *= 2;
for (int i = 1; i < n; i += 2) arr[i] /= 2;

By separating the loops based on the index set, we eliminate the need for conditional statements, which can improve vectorization and overall performance

Polyhedral Compilation

Consider the following nested loop:

for (int i = 0; i < 3; i++)
    for (int j = 0; j < 3; j++)
        x[i][j] = x[i][j - 1] + x[i - 1][j - 1];

This loop exhibits loop-carried dependences due to the use of x[i][j - 1] and x[i - 1][j - 1], which depend on values from previous iterations. Polyhedral compilation is a technique for analyzing loop dependencies and transforming loops to enable parallelization. The key idea is to represent the iteration space of a loop as a polyhedron and perform transformations on this polyhedron to eliminate dependencies.

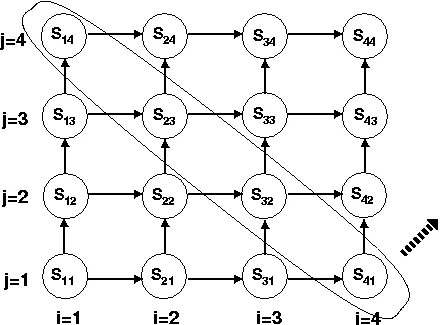
polyhedral-1

The steps involved in polyhedral compilation are:

Modeling: Map the loop iteration space onto a polyhedron, representing each iteration as a point in the polyhedron.
Dependence Analysis: Analyze the dependencies between iterations by examining the polyhedron.
Transformation: Apply transformations to the polyhedron, such as skewing, tiling, or permutation, to eliminate dependencies and expose parallelism.
Code Generation: Generate optimized loop code based on the transformed polyhedron.

Polyhedral compilation provides a systematic way to analyze and transform loops, enabling compilers to automatically identify and exploit parallelism in complex loop nests. The goal of polyhedral compilation is to teach compilers to analyze and transform loop nests automatically, leveraging the power of polyhedral representations and transformations to expose parallelism and optimize performance.

References

These notes are quite old, and I wasn’t rigorously collecting references back then. If any of the content used above belongs to you or someone you know, please let me know, and I’ll attribute it accordingly.

Kishore Kumar

Vectorization & Analyzing Loop Dependencies

Interactive Graph